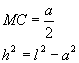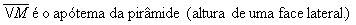Pirâmide, cone e cilindro
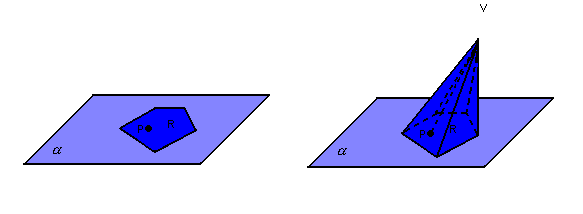
Dados um polígono convexo R, contido em um plano 
, e um ponto V ( vértice) fora de , chamamos de pirâmide o conjunto de todos os segmentos 
.
Elementos da pirâmide
Dada a pirâmide a seguir, temos os seguintes elementos:
-
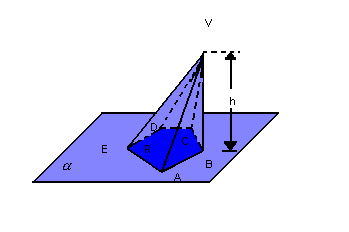
base: o polígono convexo R
-
arestas da base: os lados
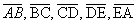do polígono -
arestas laterais: os segmentos
-
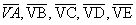
faces laterais: os triângulos VAB, VBC, VCD, VDE, VEA
-
altura: distância h do ponto V ao plano
Classificação
Uma pirâmide é reta quando a projeção ortogonal do vértice coincide com o centro do polígono da base.
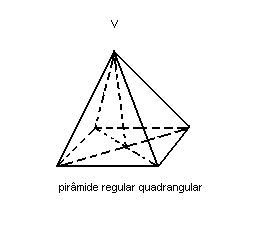
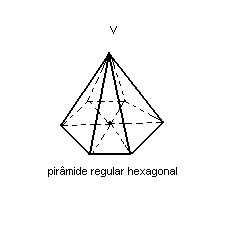
Toda pirâmide reta, cujo polígono da base é regular, recebe o nome de pirâmide regular. Ela pode ser triangular, quadrangular, pentagonal etc., conforme sua base seja, respectivamente, um triângulo, um quadrilátero, um pentágono etc.
Veja:
|
|
|
Observações:
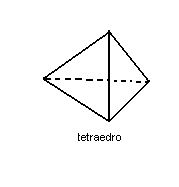
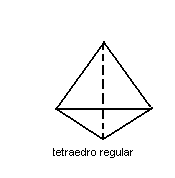
1ª) Toda pirâmide triangular recebe o nome do tetraedro. Quando o tetraedro possui como faces triângulos eqüiláteros, ele é denominado regular ( todas as faces e todas as arestas são congruentes).
|
|
|
2ª) A reunião, base com base, de duas pirâmides regulares de bases quadradas resulta num octaedro. Quando as faces das pirâmides são triângulos eqüiláteros, o octaedro é regular.
|
|
|
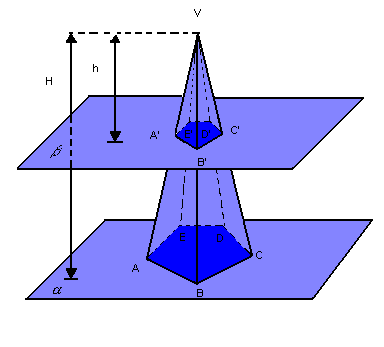
Secção paralela à base de uma pirâmide
Um plano paralelo à base que intercepte todas as arestas laterais determina uma secção poligonal de modo que:
- as arestas laterais e a altura sejam divididas na mesma razão;
- a secção obtida e a base sejam polígonos semelhantes;
- as áreas desses polígonos estejam entre si assim como os quadrados de suas distâncias ao vértice.
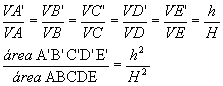
Relações entre os elementos de uma pirâmide regular
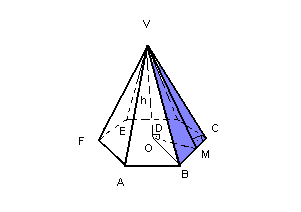
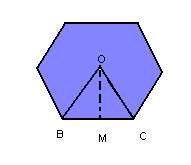
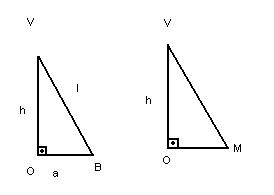
Vamos considerar uma pirâmide regular hexagonal, de aresta lateral l e aresta da base a:
|
|
|
Assim, temos:
-
A base da pirâmide é um polígono regular inscritível em um círculo de raio OB = R.
|
|
|
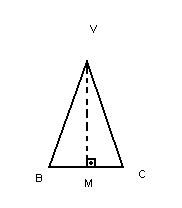
- A face lateral da pirâmide é um triângulo isósceles.
|
|
|
- Os triângulos VOB e VOM são retângulos.
Áreas
Numa pirâmide, temos as seguintes áreas:
a) área lateral ( AL): reunião das áreas das faces laterais
b) área da base ( AB): área do polígono convexo ( base da pirâmide)
c) área total (AT): união da área lateral com a área da base
AT = AL +AB
Para uma pirâmide regular, temos:
em que:
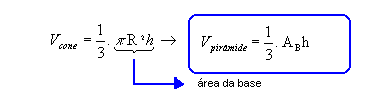
Volume
O princípio de Cavalieri assegura que um cone e uma pirâmide equivalentes possuem volumes iguais:
Troncos
Se um plano interceptar todas as arestas de uma pirâmide ou de um cone, paralelamente às suas bases, o plano dividirá cada um desses sólidos em dois outros: uma nova pirâmide e um tronco de pirâmide; e um novo cone e um tronco de cone.
Vamos estudar os troncos.
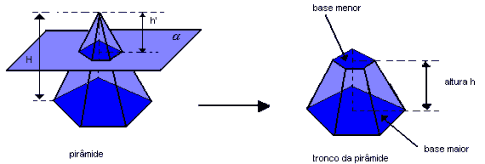
Tronco da pirâmide
Dado o tronco de pirâmide regular a seguir, temos:
-
as bases são polígonos regulares paralelos e semelhantes;
-
as faces laterais são trapézios isósceles congruentes.
Áreas
Temos as seguintes áreas:
a) área lateral (AL): soma das áreas dos trapézios isósceles congruentes que formam as faces laterais
b) área total (AT): soma da área lateral com a soma das áreas da base menor (Ab) e maior (AB)
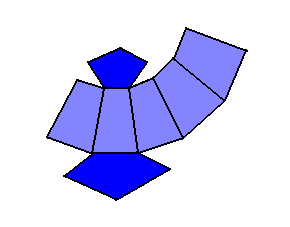
AT=AL+AB+Ab Volume
O volume de um tronco de pirâmide regular é dado por:
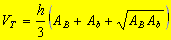
Sendo V o volume da pirâmide e V' o volume da pirâmide obtido pela secção é válida a relação:
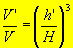
Tronco do cone
Sendo o tronco do cone circular regular a seguir, temos:
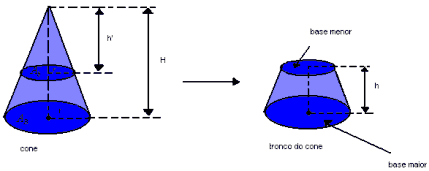
- as bases maior e menor são paralelas;
- a altura do tronco é dada pela distância entre os planos que contém as bases.
Áreas
Temos:
a) área lateral
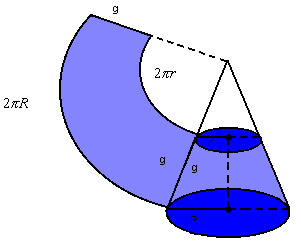
b) área total
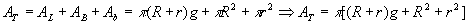
Volume
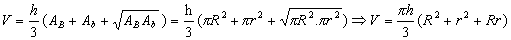
Sendo V o volume do cone e V' o volume do cone obtido pela secção são válidas as relações:
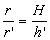
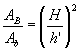
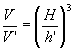
Introdução aos cilindros
O conceito de cilindro é muito importante. Nas cozinhas encontramos aplicações intensas do uso de cilindros. Nas construções, observamos caixas d'água, ferramentas, objetos, vasos de plantas, todos eles com formas cilíndricas.
Existem outras formas cilíndricas diferentes das comuns, como por exemplo o cilindro sinuzoidal obtido pela translação da função seno.
Aplicações práticas: Os cilindros abaixo sugerem alguma aplicação importante em sua vida?
A Construção de cilindros
Seja P um plano e nele vamos construir um círculo de raio r e tomemos também um segmento de reta AB que não seja paralelo ao plano P e nem esteja contido neste plano P. Um cilindro circular é a reunião de todos os segmentos congruentes e paralelos a AB com uma extremidade no círculo.
Observamos que um cilindro é uma superfície no espaço R³, mas muitas vezes vale a pena considerar o cilindro como a região sólida contida dentro do cilindro. Quando nos referirmos ao cilindro como um sólido usaremos aspas, isto é, "cilindro" e quando for à superfície, simplesmente escreveremos cilindro.
A reta que contém o segmento AB é denominada geratriz e a curva que fica no plano do "chão" é a diretriz.
Em função da inclinação do segmento AB em relação ao plano do "chão", o cilindro será chamado reto ou oblíquo, respectivamente, se o segmento AB for perpendicular ou oblíquo ao plano que contém a curva diretriz.
Objetos geométricos em um "cilindro"
Em um cilindro, podemos identificar vários elementos:
-
Base: É a região plana contendo a curva diretriz e todo o seu interior. Num cilindro existem duas bases.
-
Eixo: É o segmento de reta que liga os centros das bases do "cilindro".
-
Altura: A altura de um cilindro é a distância entre os dois planos paralelos que contêm as bases do "cilindro".
-
Superfície Lateral: É o conjunto de todos os pontos do espaço, que não estejam nas bases, obtidos pelo deslocamento paralelo da geratriz sempre apoiada sobre a curva diretriz.
-
Superfície Total: É o conjunto de todos os pontos da superfície lateral reunido com os pontos das bases do cilindro.
-
Área lateral: É a medida da superfície lateral do cilindro.
-
Área total: É a medida da superfície total do cilindro.
-
Seção meridiana de um cilindro: É uma região poligonal obtida pela interseção de um plano vertical que passa pelo centro do cilindro com o cilindro.
Extensão do conceito de cilindro
As características apresentadas antes para cilindros circulares, são também possíveis para outros tipos de curvas diretrizes, como: elipse, parábola, hipérbole, seno ou outra curva simples e suave num plano.
Mesmo que a diretriz não seja uma curva conhecida, ainda assim existem cilindros obtidos quando a curva diretriz é formada por uma reunião de curvas simples. Por exemplo, se a diretriz é uma curva retangular, temos uma situação patológica e o cilindro recebe o nome especial de prisma.
Em função da curva diretriz, o cilindro terá o nome de cilindro: elíptico, parabólico, hiperbólico, sinuzoidal (telha de eternit).
Classificação dos cilindros circulares
-
Cilindro circular oblíquo: Apresenta as geratrizes oblíquas em relação aos planos das bases.
-
Cilindro circular reto: As geratrizes são perpendiculares aos planos das bases. Este tipo de cilindro é também chamado de cilindro de revolução, pois é gerado pela rotação de um retângulo.
-
Cilindro eqüilátero: É um cilindro de revolução cuja seção meridiana é um quadrado.
Volume de um "cilindro"
Em um cilindro, o volume é dado pelo produto da área da base pela altura.
V = A(base) h
Se a base é um círculo de raio r, e pi=3,141593..., então:
V = pi r² h
Exercício: Calcular o volume de um cilindro oblíquo com base elíptica (semi-eixos a e b) e altura h. Sugestão: Veja nesta mesma Página um material sobre a área da região elíptica.
Área lateral e área total de um cilindro circular reto
Em um cilindro circular reto, a área lateral é dada por A(lateral)=2pi.r.h, onde r é o raio da base e h é a altura do cilindro. A área total corresponde à soma da área lateral com o dobro da área da base.
A(total) = A(lateral) + 2 A(base)
A(total) = 2 pi r h + 2 pi r²
A(total) = 2 pi r(h+r)
Exemplo: Um cilindro circular equilátero é aquele cuja altura é igual ao diâmetro da base, isto é h=2r. Neste caso, para calcular a área lateral, a área total e o volume, podemos usar as fórmulas, dadas por:
A(lateral) = 4 pi r²
A(base) = pi r²
A(total) = A(lateral) + 2 A(base) = 6 pi r²
Volume = A(base).h = pi r².2r = 2 pi r³
Exercício: Seja um cilindro circular reto de raio igual a 2cm e altura 3cm. Calcular a área lateral, área total e o seu volume.
A(base) = pi.r² = pi.2² = 4 pi cm²
A(lateral) = 2.pi.r.h = 2.pi.2.3 = 12 pi cm²
A(total) = A(lateral) + 2 A(base) = 12pi + 8pi = 20 pi cm²
Volume = A(base).h = pi.r²h = pi.4.3 = 12 pi cm³
Vamos estudar aqui a solução de um problema comum em postos de gasolina ou locais com recipientes cilíndricos deitados. O problema visa calcular o volume do líquido contido no cilindro deitado com comprimento igual a L e altura do líquido h.
Outro problema interessante que não será tratado aqui é o do cálculo do volume de um tanque cuja seção transversal corresponde a uma elipse em função da altura do líquido presente. Este último modelo matemático está relacionado com o cálculo do volume contido em um tanque de um caminhão.
Sugiro aos professores que acessam esta Home Page que proponham este segundo problema como um Projeto aos seus alunos de Cálculo, uma vez que são os mesmos procedimentos aqui utilizados que devem conduzir à resposta, porém a curva importante no caso será uma elipse e a mudança de variável dependerá dos parâmetros desta curva.
Nossa solução visa atender objetivos didáticos relacionados com o Cálculo Diferencial e Integral. Este problema será reduzido ao cálculo da área da região sombreada no círculo, uma vez que para este cilindro a área da seção transversal é sempre a mesma.
Para o cálculo da área, usaremos o conceito de Integral de uma função real, assunto lecionado nas primeiras séries de cursos que têm a Matemática como essencial.
Primeiramente iremos construir a circunferência de raio r com centro no ponto (0,r) e identificaremos esta região sombreada como a região localizada dentro do círculo, acima da reta y=0 e abaixo da reta y=h, onde h é a altura do líquido. A equação da circunferência será dada por:
A área da região sombreada será obtida pela integral definida:
onde a função que está sob o
